 |
Fred's Fusor
Experiments & Results |
|
Contents
of this page
 Introduction This webpage deals with experiments executed with the Fusor and with related equipment for obtaining results that demonstrate proper functioning of the equipment or for finding essential parameters to operate the equipment. Concerning the Fusor the setup parameters and the experiments are described which demonstrate fusion of Deuterium. Fusor  High Voltage Experiment/Test HV01: Testing the turns ratio of a transformer Set-up Transformer turns ratio testing (TTR testing) is performed with precise voltage meters or an inductance meter. The principle of the measurement with voltmeters is simple. By inputting an AC voltage to one coil, e.g. the primary coil, the output voltage can be determined at the other (secundary) coil. The ratio of the voltages is the turn ratio: Vin/Vout
= n1:n2
Because we are dealing with a high voltage transformer the output voltage may exceed the measuring range of the voltmeter when we put the input voltage on the primary coil. In that case the measurement could be reversed, i.e. a sufficiently high AC input voltage is put on the secundary coil and the voltage is measured now at the primary coil. Alternatively, the inductance can be measured over the open coils. This is not a reliable measurement when performed on an iron core transformer due to iron hysteresis effects that will fool the meter. Inductance is proportional to turns squared, hence the turns ratio is: n1/n2
= √L1/√L2
A cheap LRC-meter is usually not the ideal tool for measuring the inductance of a transformer coil due to its low current and usually unknown measuring frequency. Therefore we better make use of a pulse generator and an oscilloscope, which are to be connected in parallel to the inductor coil as shown in image 1. )
 Image 1: Set-up of induction measurement (© FRS 2016 The value for Ri is the output impedance of the function generator, usually 50Ω, but for our function generator it is 100Ω. The conductor L in the circuit of image 1 forms a voltage divider circuit with the resistor Ri, the impedance or internal series resistance in the function generator. With no inductance L in the circuit the oscilloscope will show the output voltage of the function generator. Connecting the inductance L into the circuit, the current through the inductor L will cause a voltage drop over Ri which will show as a lower amplitude on the scope. The current through inductor L is a function of the inductance as well as of the frequency. For a given frequency the current will be lower when the inductance is higher. At very high frequencies the current through inductor L will be negligible. For a frequency of 0 Hz (equals a DC signal) the inductor represents a short circuit. The method of measuring the inductance is as follows:
L = √(1/3) * Ri/(2*π*f)
whereL = inductance in Henry f = frequency in Herz Ri = function generator output impedance in Ohm For a function generator with an output Z (Ri) of 50Ω this will be L= 4.57/f and for a function generator with an output Z (Ri) of 100Ω this will be L = 9.19/f. Note: This method only works well with inductors with a low series resistance and an inductance ranging from about 10 to several hundreds of µH. Results Conclusion  Experiment/Test HV02: Testing the resonance frequency of an X-ray transformer Set-up The resonance point of the primary or secundary of a transformer can be tested as follows: Connect the coax shieldings of the signal/frequency generator and the scope together. Clip the scope low-capacity probe and the generator output lead across either the primary or secundary coil. Read the peak frequency at the scope. Note: a capacitor may be needed between the poles of the primary or secundaire coil to obtain an LC tank. Should the XRT have been designed for 50 Hz operation than a resonant circuit can be made with a chosen capacitor value calculated according to: F=½π√(LC) = 50 Hz
Results Conclusion  Experiment/Test HV03: Testing the performance of a transformer with different voltages Set-up For Potential Transformers (PTs) it is known that they are very robust and can be powered in reverse and by exceeding the nominal specifications. For such purposes it is required that tests are performed to establish the maximum allowable voltage to be applied to the low voltage coil, to measure the current drawn at that voltage and to measure the output on the high voltage coil. Knowing these parameters we can calculate the maximum power (in kVA) that we can obtain as high voltage output and consequently the maximum current at that high voltage output. The instruments that we need for these measurements are:
Items 2 and 3 can be combined in one instrument as shown in image 2:  Image 2: Digital Multimeter (source: supplier China) Item 4 is somewhat more difficult to realise because we want to measure a high voltage AC, whereas most HV probe meters have been designed for DC use. Usually AC high voltages are more accurately measured with a capacitive divider. Because we measure at a relatively low frequency of 50 Hz it will be possible to do the measurement by connecting a resistor with a value of 1000 MΩ (rated at 30 kV) in series with an old moving iron micro-Amp meter with a range of 0 - 50 µA. The current that flows through the resistor at a voltage of 25 kV is 25 µA and we need to replace on the meter the unit reading µA by kV to find the correct result. For safety reasons it is further advised to put a zener diode and a neon glow bulb both in parallel with the meter as a double security to conduct high voltage to ground when the meter fails and/or high voltage appears at the end of the 1000 MΩ resistor. A different approach can be chosen by connecting a series of diodes to the HV connector and measure the rectified voltage. This is not a bad solution as we intend to rectify the AC output anyway and the measurement can be done with a commercial metered probe (image 3) or a probe that can be connected to a multimeter.  Image 4: BK Precision HV probe 30 kV DC 1970's (source: supplier) Our DC high voltage probe dates form the 1970's and consists of a resistive voltage divider, contained in a long isolated stick, and an attached voltmeter. 1) The first test is to determine the performance of the Potential Transformer (PT) by measuring the ohmic resistance of the coils in an open circuit test, applying a low voltage at the low voltage coil and measuring the voltages over the other coils. This will enable us to tell someting about the performance of the TP at the arbitrary chosen, Fusor required, high voltage output of 20 kV at 20 mA. The measurement was first madse with a standard Wavetek Digital Multi Meter (DMM) but the results were inaacurate due to the own resistance of the measuring probe wires and the low ohmic resiatnce of the windings. Therefore we used a simple milli-Ohm meter and the 4-wire Kelvin method. Our milli-Ohm meter with a measuring range of 0.1 mΩ to 40 Ω with a measuring current of 200 mA is shown in image 5.  Image 5: Milli-Ohm meter R-200 (source: supplier) Results Test 1 performance of the PT: Step1: The ohmic resistance was measured over the high voltage coil, connectors A and N and found to be 8,7 kΩ; Step 2: The ohmic resistance was measured over the low voltage coil, connectors a and n and found to be 0.113 Ω; Step 3: The ohmic resistance was measured over the low voltage coil, connectors da and dn, and found to be approx. 0.224 Ω; Step 4: An AC voltage of 20 V was connected to connectors a and n; Step 5: A voltage of 11.4 V was measured at connectors da and dn; Step 6: An AC voltage of 2 V was connected to connectors a and n; Step 7: A voltage of 400 V was measured at connectors A and N. Conclusion a) The ohmic resistance of the coils is low enough to expect the PT to be able to fulfil the requirements as required for a Fusor: 20 kV at 20 mA. b) The results from step 4 and step 5 are in line with the label specifications for the PT: at an input of 20 V AC at the a and n (100/√3) coil connectors we may expect at the da and dn (100/3) coil connectors a voltage of 20 x ((100/3)/(100/√3)) = 20 x (33.33/57.74) = 11.54 V and we measured 11.4 V. This is an acceptable value in view of the measuring accuracy. c) The results from step 6 and step 7 are in line with the label specifications for the PT: with a turns ratio of 1:200 and an input of 2 V AC at the a and n low voltage coil we may expect at the A and N high voltage coil a voltage of 400V and we indeed measured 400 V. This is conform our expectations. d) The winding losses also have been calculated: with an ohmic resistance of 8.7 kΩ and a required current of 20 mA at the high voltage coil by applying Ohm's law we find a loss of 174 V, equalling a 3.48 W winding loss or copper loss, which can also be found by applying the formula
Culoss = I2R .
Similarly, with an ohmic resistance of 0.113 Ω
and an applied current of 4 A in the low voltage coil a n by
applying Ohm's
law we find a loss of 0.45 V, equalling a 1.8 W winding loss. At the
maximum allowed current of 10A the winding loss will be 11.3 W. Usually the efficiency of a transformer is calculated by the formula efficiency = 1- (losses/input).
However,
for losses in this formula we need not only to know the copper losses
but also the iron losses for which we need to know the volume of the
core. This is difficult to calculate with a PT transformer enclosed in
epoxy. By calculating the reflected impedance of the transformer we could roughly evaluate if the transformer has been properly balanced. The high voltage coil A N with an ohmic resistance of 8.7 kΩ and a turns ratio of 200 is reflected in the low voltage coil a n by R/n2 or 8700/2002 or 8.72103/4*104 which equals 0.22 Ω. The reflected impedance of 0.22 Ω is about twice the measured ohmic resistance of the low voltage coil a n of 0.12 Ω, not taking into account the presence of the second low voltage coil da dn. Test 2  Vacuum Experiment/Test V01: Testing proper functioning of a turbo pump controller Set-up A turbo pump controller, Turbo V-70 model 969-9507, was acquired from a surplus seller and prior to connecting a turbo pump to it, a test was planned to determine proper functioning (or functioning at all) of the controller. The test was found in the manual for the actual pump controller, reference 1, and this test as described in the manual was executed. Required for the test are:
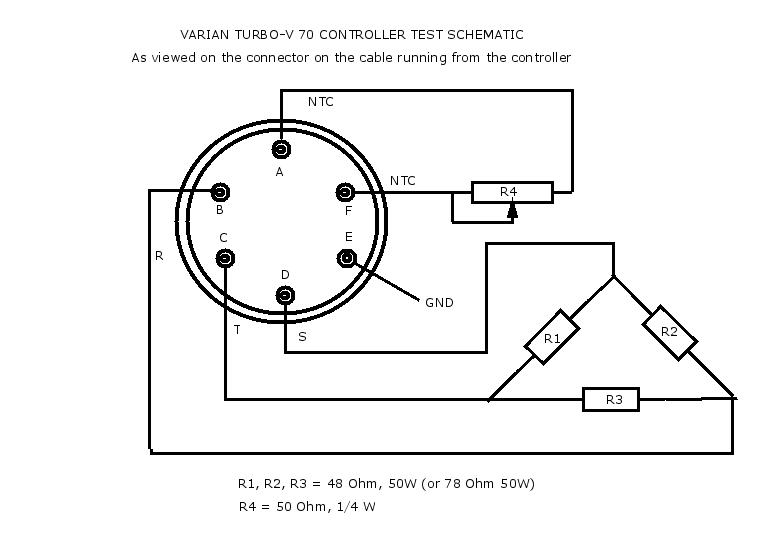 Image 6: Test set-up
for turbo pump controller (© FRS 2015)
A dummy load setup was constructed with a potentiometer of 50 kΩ and with three variable 100 Ω, 50W resistors, which were each set at 48 Ω (images 6 and 7):  Image 7: Dummy load with variable resistors (© FRS2015) Test set-up procedure:
Power supply test: a) DC voltage test Check the DC voltages referring to test points on the controller pcb. The DVM meter should read:
b) AC three-phase output voltage test On the pump connector connect the DVM in turn between: pins B and C, B and D, C and D (image 1). The meter should read 44 Vac ±15%; a different value of 1 Vac is tolerable between phase and phase. c) Front panel check On the controller front panel, press the CURRENT pushbutton and check:
Test with Dummy Load
Table 1: Test
parameters
d) Pump over-Temperature Test
The display should be as shown in the previous figure and by pressing the CURRENT pushbutton the temperature reading should be 71 °C ± 2 °C. All the other values should be zero.
e) Functional Test Perform the functional test with the turbopump, taking care to check the ramp sequence and start up time. Results Power supply test: a) DC voltage test
b) AC three-phase output voltage test
c) Front panel check Not applicable. Our controller has no front panel and is operated by a customer defined control panel. The only test possible is the 3-phase AC output voltage test with the 48 Ω dummy load and the potentiometer set at 10 kΩ:
d) Pump over-Temperature Test Lacking a front panel we only perform the 3-phase AC output voltage test with the 48 Ω dummy load and the potentiometer set at 5 kΩ:
e) Functional Test Perform as indicated. Result: Conclusion  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| References:
Ref. 1: Varian TV 70 model 969-9507 controller manual: http://ridl.cfd.rit.edu/products/manuals/Varian/other/V70(9507).pdf |
Last Updated on: Fri
Jul 24 19:48:07 2015 |