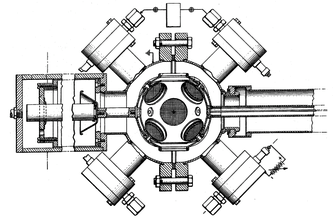
 |
Fred's Fusor
Theory |
|
Contents of this page Introduction This page of the Fusor website discusses some of the theoretical principles of fusion and in particular fusion with inertial electrostatic confinement machines. It is certainly not the intention to provide a comprehensive lecture on the theory of fusion with all possible techniques available. A large number of websites and textbooks deal with that and can easily be 'googled'. The intention of this page is to provide an overview of the mechanisms applied to our machine of choice, a Farnsworth-Hirsch type of Fusor, and to explain (some of) the rationals behind the choices made. In the introduction paragraph on the main (index, home) page of this website we mentioned a Fusor to be an inertial electrostatic confinement device in which colliding ions may fuse. The term "Inertial Electrostatic Confinement" (IEC) is used for machines of this type (belonging to the class of spherical convergent focus electrostatic ion accelerators) because a Fusor uses rather simple electrostatic forces to accelerate and confine ions and relies on the inertia of the ions to store energy for collisions. IEC's are not to be confused with Tokamaks (e.g. ITER), which use magnetic confinement and inject energy into the confined plasma in order to heat the plasma to temperatures where nuclei fuse. The basic principle of fusion is rather simple: by slamming fuel nuclei together hard enough, they will stick together and form new elements. There is, however, a limitation that tries nuclei to prevent fusing: their electric charge. Nuclei carry a positive charge and two equally charged nuclei will repel strongly, even the stronger when the distance between the nuclei becomes shorter. This is called the "Coulomb barrier", a force that needs to be overcome before fusion occurs. In a Fusor an electrical field is applied to heat (better: accelerate) ions to conditions where fusion occurs. The reactor chamber contains two concentric metal cages inside a vacuum. The metal cages have a (high) voltage potential difference, with the cathode cage inside the anode cage. It is not uncommon that the reactor chamber itself acts as the outside cage and that only one central cage is inside the reaction chamber. "Fuel" is injected as a gas into the vacuum reactor chamber, which gets ionized and as positive ions fall down the voltage drop between the outer and inner cage. Under suitable conditions they collide in the center and fuse. See reference 1 for more details.  History It was neither my intention to write an exhaustive article about the history of fusion science nor to do this for the history of the IEC type of Fusor. However, once started with sorting out historical facts about Fusors it became more and more fascinating and it certainly leads to one conclusion: full credits need to be given to the inventor of the IEC type of fusor: Dr. Philo T. Farnsworth. Let's have a closer look at him.  Image 1: Philo T. Farnsworth, January 19, 1939
(source: Harris & Ewing Collection, Lib. of Congres)
Philo Taylor Farnsworth, born August 19, 1906, is the inventor of the true electronic television, compared to earlier television systems with many mechanical parts, e.g. the rotating Nipkow disc. It is said that he came to his invention when ploughing farmland and observing the regular rows of earth covering one by one the total of the land surface. It brought him to the idea of an electron beam dissecting an image and (after transmission) synchronously building up the same image. Whether this is true or not, a fact is that at the age of 14 (i.e. in 1921) he constructed (on paper) a system to transmit electronic images over a distance. On May 13, 1930 he was granted his very first patent for an electric oscillator system, on August 20, 1930 he was granted a patent for a television system and on August 26, 1930 a patent for a television receiving system. From that time on he yielded a total of over 165 known U.S. patents and more than 300 in the rest of the world up to October 13, 1970. It is deliberately mentioned "known" patents because there may be more, especially those created in wartime and still blacklisted. He died 64 years old on March 11, 1971. See reference 2, reference 3 and reference 4. In the early 1930s Farnsworth invented a type of vacuum tube, which he called the "multipactor". This device had the ability to focus electrons at a fixed point. Farnsworth thought that this concept was suitable for keeping a plasma at a fixed place, an electrostatic plasma confinement system, into which fuel could be injected unable to escape. The concept was called a virtual electrode and the system a Fusor. By arranging several multipactors in a cylindrical arrangements it was possible to keep plasma in the center of the system, an "inertial electrostatic confinement" (IEC). In 1937 the multipactor phase control is patented as well as the multipactor oscillator and amplifier, followed by the multipactor and the multistage multipactor in 1938. In 1939 the RF frequency multipactor amplifier was patented and then war started and required other and different inventions, in particular relating to radar applications. After the war in 1949 ITT Corporation had bought Farnsworth Television Laboratories and it became difficult for Farnsworth to explore his Fusor research. Next to his professional work for ITT he worked on the Fusor in his home where he had built a laboratory. Around 1953 Farnsworth was convinced that self-sustainable fusion would be possible with his Fusor principle. The first design for a hot fusion reactor system was realized in 1958 and it was further developed up to the early 1960s. In 1959 Farnsworth moved his Fusor to a lab at ITT, who financed the project now. His Fusor however had problems when scaled up due to limitations in the amount of fuel that could be delivered into the plasma because of his ion accelator design. At that time Robert L. Hirsch was added to the research team and he improved the design by proposing a reactor with two concentric electrodes, a spherical focus diode.This diode design had been investigated by Katherine Blodgett and Irvine Langmuir in 1924 but they had not thoroughly investigated the luminescent spot that appeared in the focus of their diode, the plasma focus or Poisor as Farnsworth named it. On October 8, 1960 the Mark I Fusor produced fusion with Deuterium. Later, the Mark II, Model 2 reactor produced more than 50 Mega neutrons per second. On October 5, 1965 the Mark II, Model 6 reactor produced 1 Giga neutron per second (Gn/s) at 20 kV and 1 mA and by using Tritium as fuel and on December 28, 1965 a production of 2.6 Gn/s at 105 kV and 45 mA was achieved. This could be raised to 6.2 Gn/s at 170 kV with a mixture of Deuterium and Tritium. At the beginning of 1966 the Mark III reactor produced routinely 15.5 Gn/s at 150 kV and 70 mA. By now it was posiible to interrupt the power supply to the reactor and neutron production would continue for several seconds. This could be an indication that self-sustained fusion might be occurring. The problem left at that time was how to get consistently fuel into the core when the fusion reaction had started.  Image 2: Farnsworth
Fusor Mark II; the bell jar in the
corner is the actual reactor
Newspaper articles from that period show that ITT was being influenced by "opinion makers" to drop fusion research and Wall Street financial analysts had started expressing "concerns" about ITT. Suddenly, for the year 1966 Farnsworth was deprived from further funding by ITT who argued that fusion was "a failure..... a dead-end". Farnsworth who had invested large sums of his private money was practically bankrupt. ITT had legally asserted its complete ownership of all Fusor applications for the future and refused to sell back the patent rights to Farnsworth, who was strictly forbidden to continue any research on the "failure and dead end" Fusor. In July 1969 Farnsworth constructed a new laboratory in a cellar at Bringham Young University, Utah, and started again with Fusor research with generous support from the university and with equipment bought from private funds. Soon after his start creditors started chasing after him and he was forbidden to buy "restricted" materials such as Deuterium and Tritium, which had been regulated now by regulatory laws. Sony Corporation of Japan made him an offer but illness prevented him to accept. Shortly after the Sony offer he died at the age of 64. Gene Meeks and Robert L. Hirsch were members of the team involved at Farnsworth Fusor Research who improved the Farnsworth Fusor and which were patented: the Farnsworth-Meeks Fusor and the Hirsch-Meeks Fusor. Fusors of the Hirsch design were constructed between 1964 and 1967 but research went on into the 1970s. On December 22, 1970 patent No. 3,530,497 was granted to Robert Hirsch and Gene Meeks for an "Apparatus For Generating Fusion Reactions". The last patent of the Farnsworth Fusor era was granted to Robert Hirsch on Apr. 11, 1972: No. 3,530,497 Electrostatic Field Apparatus For Reducing Leakage Of Plasma From Magnetic Type Fusion Reactors. This patent was not relating to an IEC device but to a thermonuclear fusion reactor. The interest of the scientific world had obviously drifted to magnetically confined plasmas.  Image 3: The Farnsworth Team; l.to r.: Gene Meeks, Geo Bain, Fred Furth, Philo Farnsworth In the early 1980s a new interest started for Fusors by scientists who were disappointed by the slow progress in plasma confinement fusion reactors by George H. Miley and also from 2006 to his sudden death in 2007 by Robert W. Bussard, who was granted patents No. 4,826,646 on May 2, 1989, Method And Apparatus For Controlling Charged Particles and No. 5,160,695 on Nov. 3, 1992, Method And Apparatus For Creating And Controlling Nuclear Fusion Reactions. Since the 1990s amateurs are constructing home-made Farnsworth or Fransworth-Hirsch Fusors with Richard Hull of Richmond, Virginia, being the first amateur who achieved Deuterium fusion in a Fusor. On October 19, 2012, Robert L. Hirsch gave a lecture for the 14th U.S.-Japan IECF Workshop with a rather surprising message. This integral lecture can be found on a separate page of this website: the Hirsch Page (button below). It is advised to read his words.  What can be learned from Hirsch's words and what is his professional or social status nowadays? The key elements from the Hirsch speech are:
Robert L. Hirsch has been a manager of petroleum exploratory research at Exxon, a senior staff member at the RAND Corporation, and director of the US research program on nuclear fusion energy. In 2005 he published a report on "peak oil" for the U.S. Department of Energy (DoE). According to Hirsch oil production has reached a peak and production will start declining between 2011 and 2015 causing unpleasant consequences for nations and individuals. See refererence 5 and reference 6. Furthermore, Robert Hirsch has the opinion that in Washington a conspiracy is going on to keep the "peak oil" issue quiet. This ends our historical overview of Fusor history.  |
| Theory of
Fusion Requirements for Fusion It is generally agreed that in order to obtain a thermonuclear fusion (i.e. in a magnetically confined plasma) the temperature of the nuclei needs to be raised to an ignition point, or that -in other words- the nuclei must contain sufficient energy to fuse. Heat and pressure are also present in an IEC reactor, which instead uses acceleration of the velocity of nuclei (ions) and increasing the density of nuclei in the center of the device for fusing these nuclei and not just (Maxwellian) heat. Temperature is the average kinetic energy per unit volume and the conversion ratio of 1 eV = 11604.45 K. See reference 7. The unit used here for temperature is Kelvin, which is the common unit used for scientific purposes. For conversion to centigrades: 1°C = 274.15 Kelvin or in general: °C - 274.15 = K and K + 274.15 = °C. Should we apply a potential difference of 30 kV in a Fusor and an electron is accelerated between these two electrodes than the electron would gain 30 keV, which is equivalent with a temperature rise of 3.5*108 K. When considering Deuterium as fuel in a thermonuclear fusion and starting with a mass of Deuterium at standard (ambient) temperature and pressure, a temperature of 108 K in the mass will cause some of the Deuterium atoms to fuse and to release energy. The pressure of the mass at that temperature will be near 1.5*105 bar. At that temperature the reaction is not self-sustaining. A self-sustaining reaction should theoretically occur at a temperature of 3.5*108 K. Two facts are revealed by the foregoing temperature and pressure relations:
So far we have defined that our Fusor needs to operate at a high vacuum to permit amongst others not only the pressure rise from fusion but also to prevent that the fuel becomes contaminated with non-fuel ions and that we will need an inertial electrostatic confinement of the plasma in order to keep it focused in the center of the vacuum chamber to prevent it from cooling down or destructing the chamber. For creating an inertial electrostatic confinement as well as for accelerating the velocity of the nuclei to fusing energies we need to apply a high voltage. The high voltage will have to be applied to electrodes and in our Fusor the electrodes are concentrically arranged in the vacuum chamber with the cathode inside the anode. In fact, the outer wall of our Fusor is the anode and in the center of the spheroidal vacuum chamber the relatively transparant grid shaped cathode is located, connected to a high voltage vacuum feedthrough in the outer wall of the chamber. Furthermore we will need to inject a fuel into the Fusor for obtaining nuclei that can be accelerated. The rational for the choice of the fuel is discussed in one of the next chapters. Arriving at this point the conclusion might be drawn from the first paragraph of this chapter that obtaining a self-sustaining fusion of deuterium nuclei can rather easily be achieved by applying a potential difference of 30kV between the electrodes, because it was mentioned that a self-sustaining reaction will occur at a temperature of 3.5*108 K and 30,000 Volt multiplied with the conversion ratio of 1 eV of 11604.45 K will yield 3.48*108 K. This is, however, not the case for a number of reasons, with the most important reason being the presence of the cathode grid, which "absorbs" quite a large amount of the positively charged deuterium nuclei when they hit the grid. The Lawson Criterion for fusion power is Fusion
Power = Efficiency * [Fusion - Conduction - Radiation]
In grid operated systems conduction losses will be very high and for a true fusion reactor we will have to get rid of the grid. In an operating Fusor when e.g. Deuterium gas is fed into the vacuum chamber the gas molecules will become ionized by the high voltage electric field between the anode wall of the vacuum chamber and the cathode grid and Deuterons are formed (i.e. Deuterium ions with a charge of 1+). For all types of accelerators an electric field will increase the kinetic energy of charged particles according to 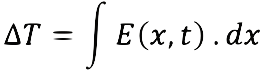 (integral taken along the particle orbit where in the most general case E varies in time and position). In the special case of an electrostatic accelerator consisting of two conducting surfaces with a large voltage difference V0, a particle with charge q gains a kinetic energy qV0. Deuterons travel as positively charged nuclei towards the neagtive spherical cage cathode gaining speed until in the center of the spherical cage cathode a nucleus hits another charged, accelerated nucleus and - by breaking the Coulomb barrier- the two nuclei fuse. The center of the spherical cage cathode is a potential well and the place of the plasma focus or Poisor. Nuclei which miss a collision will travel through the potential well towards the opposite wall, loosing their speed (as these positively charged nuclei are travelling towards a repelling positively charged wall) until the negative force applied by the cathode wins and the nuclei inverse their direction and start travelling towards the cathode again and gain speed for another possible collision. This will continue until all nuclei have collided and are converted by fusion in other elements and will have released energy. The meaning of "potential well" is demonstrated in image 4, though this "negative electrostatic apparatus" works slightly different than the Fusor as described on this website. The device in image 3 has electrons injected radially inward to the center of the spherical shell screen grid system with the grid (100) at a high positive potential relative to an electron emitting outer surface shell (110, at ground potential) surrounding the grid. Electrons are being injected into the interior grid space with the energy of the potential difference (120) between grid and outer shell. The diagram below the apparatus shows the potential distribution in this device, which is a spherical electron accelerator based on the Elmore,Tuck and Watson concept of 1959. In our Fusor a similar potential well is created but here the bottom of the well is at a high negative potential relative to the tops of the curve (at ground potential). In the Fusor positively charged ions will "fall" of the hill towards the bottom of the well and in case of not hitting (an)other ion(s) coming from a different direction and fusing, they will "climb" up the slope of the well until sufficiently "braked" and start "falling" again down the hill, ready for another attempt to fuse. As we will see later on this page the 'main power' behind the process of recirculating ions is the fact that due to the low pressure in the Fusor the mean free path of the ions has extended to a lenght that exceeds the diameter of the (spherical) Fusor and the particles are just travelling to complete the mean free path, helped by electrostatic field forces, attracting and repelling the charged particles (in our case: ions). 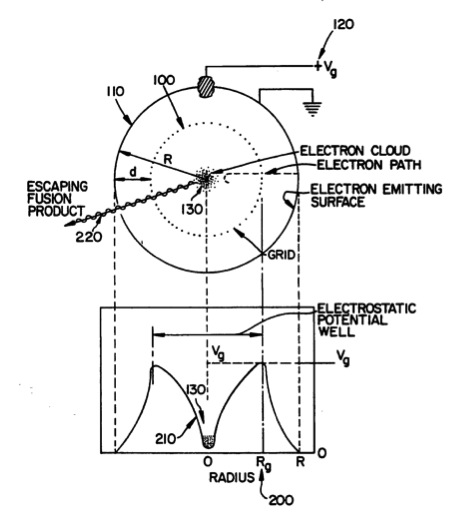 Image 4: Electrostatic
potential well (source: U.S. patent 5,160,695 by R.W. Bussard)
As mentioned before, a 100% conversion of injected fuel does not occur because of grid lossses by nuclei colliding with the grid and therefore a breakeven point will never be reached by this system of Fusor. In fact, the majority of deuterons will slam into the grid and wil get lost. The phenomenon of developing an effective grid with a minimal 'presence' is known as grid transparancy and it is a factor in the design of a Farnsworth-Hirsch Fusor. It is therefore evident that for enabling an at breakeven point operating Fusor wasting the drive energy has to be resolved and that means to get rid of the grid. Systems have been developed wthout a grid but they are not within the scope of this project. It is emphasized here that our project does not have the intention to construct an IEC device that comes even near the breakeven point as this generates very high amounts of undesirable (fast) neutrons. Our sole and only purpose with the project is to demonstrate that nuclear fusion can be achieved with simple means and low funding.  Ionization of Fuel Atoms In order to operate the Fusor it needs a supply of nuclei to be accelerated, a fuel, which is fed into the Fusor as a gas that will become ionized. Because the Fusor operates under a high vacuum, the fuel gas is "leaked" into the vacuum chamber (reactor) by means of a precision regulated valve. The ionization of gas molecules, e.g. Deuterium gas, occurs in a sufficiently strong electrical field wich is created between the outher wall of the vacuum chamber, the anode, and the inner grid, the cathode. When a sufficient amount of energy is transferred to a bound electron, i.e. when the threshold of the ionization potential is exceeded, a free electron is created which will drift towards the anode leaving a positively charged ion which will drift towards the cathode. In a sufficiently strong electric field the liberated electron will gain sufficient energy to liberate a further electron when it collides with another molecule and the process of gaining energy now proceeds for two elctrons which will liberate each another electron, and so on. Free electrons not only originate directly from ionized gas but are also generated by cosmic rays colliding with gas molecules and thus exciting them to higher energy states. The free electrons originating from cosmic rays interaction are called "seeding electrons" because they are at the basis of the process of generation of secundary free electrons. Another source of free electrons is the cathode (grid) in the Fusor, which releases electrons when under high voltage.This chain reaction of electron generation is called a Townsend avalanche. It depends on the free electrons gaining sufficient energy between collisions to sustain the avalanche. See reference 8. The final state of the Townsend avalanche is the Townsend breakdown, which is the situation when the gas suddenly changes from being a dielectric to a conductor by clouds of free electrons conducting the current between cathode and anode. The next step in the ionized gas process is formation of a plasma, another fundamental state of matter next to solid, liquid and gas. A plasma has similar conductive properties to that of metals and this can be observed by a sudden raise in current between the electrodes once the state of plasma has occurred, possibly followed by plummeting of the voltage (depending on the type of HV power supply). See reference 9. Characteristics of a plasma are the high electrical conductivity and the response to magnetic fields. Plasma is usually quasineutral, i.e. positive and negative particles are more or less in equilibrium. However, plasma of monocharged particles do exist but the density must generally be very low, or it must be very small, otherwise it will be dissipated by repulsive electrostatic force. For plasma to exist, ionization is required and the degree of ionization is the proportion of atoms that have lost or gained electrons and is controlled by the temperature of the plasma. An inert electrostatic confinement plasma can have a particle density of 1032 per m3 and the temperature of the same plasma can reach 108 Kelvin. In an IEC device the plasma concentrates in the center of the hollow cathode, the Poisor, basically a spherical focus diode. When pressure in the vacuum chamber and high voltage have the right conditions the ion density in the Poisor increases until a glowing ball of plasma will be formed. When the plasma is fed with a higher grid voltage with a correspondingly higher current a dense plasma focus will result and a plasma-magnetic entity will be formed in the Poisor: a plasmoid. The plasmoid goes through different shapes when the power is further raised: bugle mode, jet mode and star mode. In bugle mode the ball shaped plasmoid has a trumpet-shaped ion blow-out, in jet mode the ion blow-out is a sharp line and in star mode brilliant rays are ejected from each aperture of the inner grid. At higher pressures and at a too high starting potential electric discharges may occur before the Fusor comes into glow discharge mode: Depending on the pressure of the gas in the vacuum chamber, the voltage applied between cathode and anode and the distance between these electrodes, an electric discharge through the plasma and the avalanching free electrons cloud may occur. An electric discharge is however not what we want in an operating Fusor and it is therefore desirable to know the conditions under which discharges may develop. The voltage necessary to start a discharge or electric arc, between two electrodes in a gas as a function of pressure and gap length is called the breakdown voltage (as described above) and can be defined by an equation known as Paschen's Law: 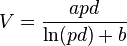 V = breakdown voltage in volts p = pressure in bar d = gap distance in meters (i.e. distance between anode and cathode in the Fusor) a and b are constants depending on the composition of the gas The breakdown voltage depends on the mean free path (MFP) of the particles which increases with decreasing pressure. The MFP is the average distance a particle travels before colliding with another particle. The relationship between pressure and voltage is flat at higher pressures, goes through a minimum voltage, and then asymptotically rises as the mean free path exceeds the electrode spacing. A graph based on the equation is the Paschen curve, as shown in image 5 for a number of gases.  Image 5: Paschen curves obtained for helium, neon, argon, hydrogen and nitrogen, using the expression for the breakdown voltage as a function of the parameters A,B that interpolate the first Townsend coefficient. Source: reference 10. The breakdown voltages in the curve from image 5 have been drawn for gases that are not of interest for use as fuel in a Fusor. We have collected some data for Deuterium and plotted a graph as shown in image 6:  Image 6: Breakdown voltage
for Deuterium. Source: reference 11.
Graph © FRS 2014
The graph of image 6 shows that for the high voltage region of interest (ROI) for a Fusor, 26 to 30 kV, the voltage breakdown for Deuterium occurs at absolute pressures ranging from 7 to 16 mbar cm. It is difficult to draw conclusions from these data because not much has been published on the relationships between voltage, current and pressure in IEC devices. The graphs relating to Paschen's Law are based on measurements with flat plate electrodes but in an IEC reactor the cathode is spherical and hollow. It is, however, known that the geometry of the electrodes have a significant effect on the results (streamer discharge concept). The Townsend breakdown mechanism is only valid for slowly rising voltages and low pressures. The resulting discharge is diffuse of shape. At fast rising voltages and when the product between pressure and anode/cathode distance is sufficiently large, a distortion of the electrical field may occur yielding a filamentary channel (or streamer) bridging the anode/cathode gap. When we summarize our findings from these first two chapters it becomes clear that:
 Choice of Fuel Fusion, as mentioned before, is the process of combining nuclei in order to make heavier elements and to release energy, i.e. the process is exothermic. Conventional nuclear reactors produce energy by fission of nuclei and they use heavy elements for that process. Contrary to fission, which uses heavy elements as "fuel", a Fusor uses light elements for fusion. In image 7 the binding energy per nucleon, expressed in MeV units, has been plotted against the number of nucleons (the sum of protons and neutrons) per nucleus. When nucleons, such as protons and neutrons, are added to a nucleus, the nuclear force attracts the added nucleon to other nucleons, though primarily to its immediate neighbours due to the short range of the force. Nucleons on the surface of the nucleus have less neighbouring nucleons than those on the interior of the nucleus. Due to the nuclear force the binding energy per nucleon increases with the size of the nucleon because smaller nuclei have a larger surface area to volume ratio than larger nuclei. The size of the nucleus, however, has a limiting value that corresponds with the size of a nucleus with a diameter of about four nucleons. A different force occurring in the nucleus is the electrostatic force (an inverse-square force) caused by electrostatic repulsion between protons present in the nucleus. The net result of all opposing forces in the nucleus is generally that binding energy per nucleus increases with increasing nucleus size up to the elements iron and nickel and then decreases for the heavier nuclei. Eventually, the binding energy becomes negative and nuclei become instable when the number of nucleons exceed 208, which corresponds with a diameter of 6 nucleons.  Image 7: Binding energy per
nucleon
The graph has Iron-56 marked to indicate the nuclides with the highest binding energy per nucleon, followed by Iron-58 and reaching a maximum at Nickel-62. Elements with a lower number of nucleons in the nucleus than Iron-56/Nickel-62, i.e. in the graph to the left of Fe56, release energy when subjected to fusion. Elements with a higher number of nucleons in the nucleus than Iron-56/Nickel-62, i.e. in the graph to the right of Fe56, release energy when subjected to fission. This is very much generalized because in the top of the curve there is not much energy to be gained from fusion or fission. A fission nuclear reactor works without exception with nuclides containing 233, 235 or 239 nucleons in the nucleus. Iron-56 has been marked in the graph as the stable nuclide with the highest binding energy because Nickel-62 (which has in fact the highest binding energy) is in natural sources less present, indicating that it is less likely to be formed in natural processes. Iron-56 is by far the most found element on earth. The conclusion that should be drawn from the plot of binding energies is that for our (amateur) fusion purposes we will have to find our fuel in the lighter elements and preferably in the lightest, ranging from H1 to H3, because they will require the lowest energy input for fusion or, with other words, the fusion reactions peak at relatively low temperatures (= kinetic energy). Image 8 shows the fusion rates, expressed as m3 per second versus the temperature in Kelvin and the kinetic energy in keV, for Deuterium-Tritium, Deuterium-Deuterium and Deuterium-Helium-3 fusion reactions. 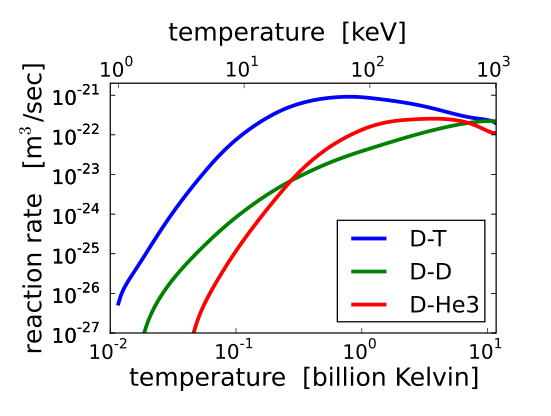 Image 8: "Fusion
reaction rate", Source: reference 12
In the graph from image 8 the fusion reaction rate increases rapidly with temperature until it maximizes and then gradually drops off. The DT rate peaks at a lower temperature (about 70 keV, or 800 million kelvin) and at a higher value than other reactions commonly considered for fusion energy. This makes the DT reaction a preferred choice for current Tokamaks under construction (e.g. ITER). Image 8 is a plot of the fusion reaction rate (average of cross-section times speed) vs. temperature for three common reactions. The average is over Maxwellian ion distributions with the appropriate temperature. The plot was made by Dstrozzi with scientific Python tools using data from the NRL Plasma Formulary, 2006 revision. In institutional fusion research, fusion reactions up to the element Boron-11 are being considered, mainly because a high interest exists for aneutronic fusion reactions (reference 13). Where amateur fusioneers look for reactions where neutrons are being produced, because measuring neutron generation is a means that indicates that fusion has occurred, for commercial energy production aneutronic fusion reactions are increasingly getting more attention. The reason that neutrons are unwanted is that neutrons in high amounts are dangerous to health and therefore will require expensive shielding, but even more important is the fact that neutrons generate high amounts of γ-radiation when hitting metal components of the fusion reactor and this makes the outer shell of the reactor radioactive (generating radioactive waist) and it will cause structural damage by dislocating atoms in the metal lattice, which will weaken the strength of the metal reactor components (reduction of operational lifetime). When considering the choice for the appropriate light element for fusion it should be recognized "that conventional magnetic confinement approaches to fusion power generation are practically unable to take advantage of the large energy gains (G=ratio of energy output to energy input per fusion reaction) naturally found in the fusion reactions between various reactive isotopes of the light elements These gains can be as large as G≈1000-2000 for the fusion of deuterium (D or 2H) with tritium (T or 3H), the two heavy isotopes of hydrogen (p or 1H), according to D+T→4He+0n (+17.6 MeV), or up to G≈50-100 for fusion between hydrogen (p) and boron-11 (11B), p+11B→3 4He (+8.6 MeV). In spite of this, it is found that the large power requirements for confinement and plasma heating in magnetic confinement approaches place practical engineering limits on the energy gain potentially achievable to 2<G<5" (source: reference 14). It is clearly stated here that the natural large energy gains from the fusion reactions are partially consumed by the power requirements needed for generating the plasma confinement and the plasma heating. Considering the differences in the energy gain for the D-T reaction compared to the p-B reaction it is understandable that in international research projects at a potentially achievable gain of 2<G<5 the choice is made for the higher gain D-T reaction, taking the disadvantage of neutron production as a side effect. The question now could be why amateur fusioneers prefer to use the D-D reaction instead of the D-T reaction and also why research institutes do not consider the p-p reaction. To find the answer we shall have a closer look now at the individual reactions, starting with the lightest elements.  Image 9: Cross sections of
fusion reactions (source: reference 15)
 Proton-Proton Fusion Fusion reactions converting Hydrogen into Helium take place inside the Sun and in stars of similar mass. The chain of reactions from Hydrogen to Helium is called the proton-proton chain. It starts with the reaction: 1H + 1H
→ 2H + e+
+ ve + (0.42 MeV)
The nucleus of Hydrogen consists of one proton with an electric charge of 1.6 x 10-19C. When two protons fuse, a Deuterium nucleus is formed (an isotope of Hydrogen with one proton and one neutron in the nucleus) together with one electron, one neutrino and 0.42 MeV of energy is released. According to classical mechanics a very high temperature is required to fuse two protons. In fact, the temperature of the Sun is not high enough to perform fusion by the classical mechanics process. In the Sun fusion of protons occur by quantum tunneling. The quantum tunneling process relies on weak nuclear interaction and therefore have a very low probability to occur. When a proton through tunneling overcomes the Coulomb barrier and ends up beside a second proton laws of physics do not permit that a double proton state exists and therefore almost immediately one of the protons undergoes a weak interaction to become a neutron, yielding a stable state of proton plus neutron, which is Deuterium. The probability that tunneling of protons occur is an average of once in 3.16 x 1017 seconds. The extremely high temperature as required by classical mechanics and the low probability of quantum tunneling at lower temperatures makes the proton-proton fusion a non-preferred reaction for fusion in reactors. Simpler said, and taking the mass/velocity relationship into account, a proton has insufficient mass for acceleration to the required speed (kinetic energy) needed for fusion by means of a Fusor.  Deuterium-Deuterium Fusion The D-D fusion has an optimum energy to initiate the reaction at 15 keV and has two stages in which fusion may occur. The first stage has two processes with equal opportunity to occur: 2H + 2H
→3H (1.01 MeV) + p+
(3.02 MeV) (50%)
and 2H + 2H
→ 3He (0.82 MeV) + n
(2.45 MeV) (50%)
In the second stage two reactions may occur: 3H + 2H
→ 4He (3.517 MeV) + n (14.069 MeV)
and 3He + 2H
→ 4He (3.6 MeV) + p+ (14.7 MeV)
In the second stage Tritium as formed in the first stage may fuse with Deuterium present in the reactor yielding Helium-4 and emitting a neutron with high energy. This reaction is likely to occur because the minimum energy required for D-T fusion is lower than that for D-D fusion. The second stage reaction where formed Helium-3 fuses with Deuterium present in the reactor is less likely to occur becuse in this case the peak reaction rate energy required for fusion is much higher than for the D-D reaction. Neutrons emitted from the D-D reaction are slightly peaked in the forward (along the axis of the ion beam) direction. In both cases, the associated He nuclei are emitted in the opposite direction of the neutron. In a Fusor with a spherical focus diode as cathode the Deuterons come from all sides towards the cathode and therefore neutrons will be emitted randomly in all directions. The D-D reaction is in favour by amateur fusioneers because Deuterium is easily and relatively cheap available as gas and also as a liquid Deuterium oxide (heavy water). When obtained as heavy water, Deuterium gas needs to be produced by electrolysis to make it suitable for feeding into the reactor. Deuterium is present as a natural resource in hughe quantities. It is present in the world's oceans in a mean ratio of 156 atoms Deuterium per one million Hydrogen atoms (156 ppm) and it can be extracted from sea water as Deuterium oxide (Heavy Water) or as Deuterium gas.  Deuterium-Tritium Fusion The Deuterium - Tritium reaction is a fusion process between the two heavy isotopes of Hydrogen: 2H + 3H
→ 4He (3.517 MeV) + n (14.069 MeV)
The reaction produces Helium-4 and releases a high energy neutron. For fusion research the D-T reaction is more in favour than the D-D reaction:
6Li + n → 4He + 3H
+ (4.08 MeV)
An advantage of the Lithium blanket is that neutrons from the D-T recation will be absorbed, and by doing that the blanket acts as a shielding for the neutron flux from the reactor. The problems in designing the Lithium blanket and optimizing it for the fusion process are, however, bigger than designing the actual tokamak reactor itself. The reason is that neutrons with different energies are emitted from the D-D and D-T reactions in a thermonuclear reactor and for reacting with Lithium to obtain a high Tritium breeding ratio, a mixture of Lithium isotopes will be required. Another way to induce a large Tritium breeding ratio is by doping the Lithium blanket with neutron multipliers such as Beryllium and Lead, The fact that 80% of the energy is carried away by the emitted neutron means that only 20% of the energy remains intact in the plasma, yielding ignition problems to keep the reactor going. A very high neutron flux from this reaction causes damage to the structural elements of the reactor, unless these neutrons will be absorbed by a Lithium blanket. Because of the limitations existing for Tritium (radioactive, licence required for buying and handling) the D-T reaction is not suitable for the amateur fusioneer.  Deuterium-Helium-3 Fusion In the D-He3 fusion reaction, Deuterium is fused with the lightest isotope of Helium, Helium-3, in a reaction which peaks at a relatively high energy of 58 keV: 2H
+ 3He → 4He
(3.6 MeV) + p+
(14.7 MeV)
Despite the fact that the fusion reaction is aneutronic, the relatively high reaction temperature is a disadvantage compared to the D-D and the D-T reactions. Another disadvantage is that Helium-3 is very scarce because it is a decay product of Tritium, which is formed as a byproduct in fission reactors. Helium-3 is produced in extremely low amounts. The main pathway of the D-He3 reaction does not produce neutrons, but side reactions will do, such as the D-D reaction and (less probable) the D-T reaction as the second stage reaction from the D-D reaction. The reduced amount of neutrons from the D-He3 reaction and its side reactions will reduce the costs of shielding the reactor. An advantage of the D-He3 reaction is the possibility of direct conversion of energy by means of a process of extracting energy from fast moving charged particles and converting this into electricity. Normally, energy is extracted indirectly from fusion or fission processes by means of a heat transfer exchange from a heated coolant and converting this into electricity through steam turbines and generators. The efficiency of the thermal conversion process is ussually 40-50% whereas the direct conversion of energy may have an efficiency of > 90%.  Helium-3-Helium-3 Fusion This reaction is mentioned here only for completenes of fusion reactions with the lightest elements. The scarcity of Helium-3 makes this reaction just as impractical as the D-He3 reaction mentioned before. The reaction yields Helium-4 and it peaks at an even higher energy than the p-B11 reaction (see image 8): 3He + 3He
→ 4H + 2 p+ (12.86 MeV)
The scarcity of Helium-3 and the high energy required for fusion make this reaction a theoretical option only.  Proton-Boron-11 Fusion The p-B11 reaction is considered as an aneutronic fusion reaction with a first peak energy at 123 keV, a second peak energy at 600 keV and (nevertheless) a neutron emission rate of 0.001, i.e. every thousand fusion reactions will yield one neutron. The reaction yields 3 Helium-4 nuclei and energy: p+ + 11B
→ 3 4He
+ (8.7 MeV)
At first sight with one Boron-11 nucleus delivering 3 Helium-4 nuclei the reaction looks like a fission reaction. This is, however, not the case because in the first stage of the reaction an instable Carbon-12 nucleus is formed by fusion, which is proton/neutron instable and in the second stage immediately decays into three α-particles, which are Helium-4 nuclei (2 protons and two neutrons). The claimed aneutronicity of the reaction is valid for the main reaction, but side reactions may yield low energy neutrons or hard gamma's (reference 16): α + 11B →
14N + n
1p + 11B → 11C + n 1p + 11B → 12C + Υ The peak energy of the reaction is at 600 keV considered as quite high (Image 9) and it will require a totally different reactor design. The advantages of being an aneutronic reaction, the high availability of Boron and the fact that the reaction product consists of charged particles (enabling direct conversion into electricity) makes the reaction quite desirable for commercial fusion applications, though the engineering problems to design a p-B11 reactor are currently quite 'unresolvable'. One of the designs currently under development is the Polywell (reference 17). Boron is present in hughe quantities as a natural resource. The proven mineral mining reserves are more than one billion metric tonnes and current yearly production ia about four million tonnes. Turkey has 72% of the world's known deposits, followed by the U.S.A. as the second large source (reference 18).  Muon-Catalyzed Fusion For completeness we mention here also Muon-catalyzed fusion as a possibility for a fusion process, though it is absolutely not within reach of amateur fusion. A muon is an elementary particle similar to an electron with a charge of -1 but with a far higher mass (105.7 Mev/c2) and a mean life time of 2.2 µs (reference 19). The mass of a muon is about 200 times that of an electron and when a muon orbits a nucleus this will be at 1/200th of the distance that an electron does. This will lower the Coulomb barrier substantially and therefore fusion can be accomplished at lower temperatures. Unfortunately muons suffer from α-sticking caused by the fact that α' s have a charge of 2+ and adhere more easily to muons than protons do with a charge of 1+. The α-particles do not undergo fusion under these conditions and the muons get lost due to decay. Currently, research projects have achieved somewhere around 200-300 fusions per muon, which will have to be raised to more than 500 fusions per muon before the energetic costs of production are amortized, which is 6 GeV per muon and that is far more than the net energy gained from muon catalyzed fusion. The process is considered to be far from economical. ≈
Conclusions: For a Farnsworth-Hirsch Fusor built and operated by the amateur fusioneer only the Deuterium-Deuterium reaction appears to be of interest:
 Choice of Energy The fusion process in the Fusor is thermonuclear fusion, or hot fusion, not to be confused with cold fusion processes or low energy nuclear fusion (LENR). In our Fusor we apply a voltage of (e.g.) 25 kV and an electrostatically accelerated Deuteron (an ion with a charge +1) which passes through the grid has gained a kinetic energy of 25,000 electronvolts (25 keV). When multiplied with 11,604 to obtain Kelvin we find that in the heart of our Fusor a temperature exists of more than 290 million degrees Kelvin. Somewhat surprisingly it is not heat that is the key to achieve fusion but it is velocity caused by electrostatic acceleration. From the Maxwell–Boltzmann distribution (or Maxwell speed distribution) for particle speeds in idealized gases the following equation for velocity v of a particle was developed:
where: v is velocity of a particle K is the Boltzmann constant=1.4*10-23 JK-1 m is the mass in kg T is the temperature in K. The equation shows that a direct relationship exists for the velocity of a particle and temperature and also that heat is a means to achieve speed (and vice versa as shown in our 25 keV Fusor example above). It appears that this is a very crucial point because large governmental institutions are struggling for decades now to achieve fusion by heating gas with convential means in tokamaks (e.g. ITER) and high power lasers (e.g. HiPER), whereas the answer may be found in using a more simple and direct way to obtain high velocity by using electrostatic acceleration. At fusion energies (> 10 keV) the fusion reactants exist in a plasma state because the ionization energy for Deuterium of 15.47 eV is highly exceeded. The plasma in a Fusor turns into a Poisor (a plasma focus, plasmoid) when a mean free path for particles (ions) has been reached comparable to the vacuum chamber radius. In general, extending the mean free path of particles is achieved by lowering the pressure in the vacuum chamber as can be derived from equation II, the equation for calculating the mean free path of a particle:
where: l is the mean free part for particles kB is the Boltzmann constant in Joule per Kelvin (1.3806488(13)×10−23 JK-1) T is the temperature in Kelvin d is the diameter of gas particles in meters p is the pressure in Pascal Reference 20 also gives some mean free path values for air at room temperature at different pressures, which have been listed in table 1:
Table 1: Mean free path values
for air at ambient temperature at different pressure (source: reference 20)
When the mean free path of a particle in a sphere shaped Fusor exceeds approximately three radii, the particle will start recirculation and when the pressure is further lowered (i.e. the mean free path further enlarged) the particle will start to oscillate back and forth through the plasma focus until the mean free path has been reached or until a (negatively charged) cathode wire of the grid is met and the (positively charged) particle ceases to exist (reference 21). As we have seen in the preceding paragraph recirculation of ions occurs when the mean free path of the ions exceed the diameter of the vacuum chamber; after all the particles cannot escape from the vacuum chamber to accomplish their mean free path. Therefore, particles which have passed the plasma focus will decelerate, reverse their direction and accelerate again towards the plasma focus, taking another opportunity to collide and fuse or to end their existence as an ion when caught by a grid wire. In a Farnsworth-Hirsch Fusor an ion generally makes about five recirculation passes before it ends against the grid. In an ideal situation a grid wire should be infinitely thin, which is impossible, and the concept of grid transparancy has been developed for constructing a grid with the best possible open structure for the Fusor. This will be discussed in the next chapter on this page: Grid design. The general rule of five recirculation passes proved to be incorrect when the grid is geometrically good designed and accurately placed in the vacuum chamber. Very precisely adjusted Fusors may show the George Miley effect, where the plasma turns into the "star" mode. Apparently this is a phenomenon where ions seem to avoid hitting the grid and will travel through void places in the grid and form star-like rays, which named this plasma mode (reference 21). The equation that defines fusion rate for a plasma with a constant particle density is:
or, when taking into account that particle velocity in general has a Maxwellian distribution it makes sense to average σv over the integral region of the relative velocity:
where: f is the fusion rate or reaction rate (fusions per volume per time, i.e. per cm3 per second) n1 and n2 are the densities of two colliding ion species in particles per cm3 σ (sigma) is the reaction cross section in barns v is the relative particle velocity in cm/sec It should be noted here that nowhere in the equation (II or III) temperature appears because the fusion process deals only with densities, dimensions and velocity (reference 22). The term (σv) is called the reactivity, the appropriate average of the fusion cross section σ over the relative velocities v, expressed in units of cm3 /sec. A plot of reaction rates versus kinetic temperature is shown in image 10, similar to images 8 and 9.The plot clearly shows that D-D fusion rates increase with increasing energies (temperatures): at 10 keV just over 10-24 m3/sec and at 30 keV approximately 10-23 m3/sec. 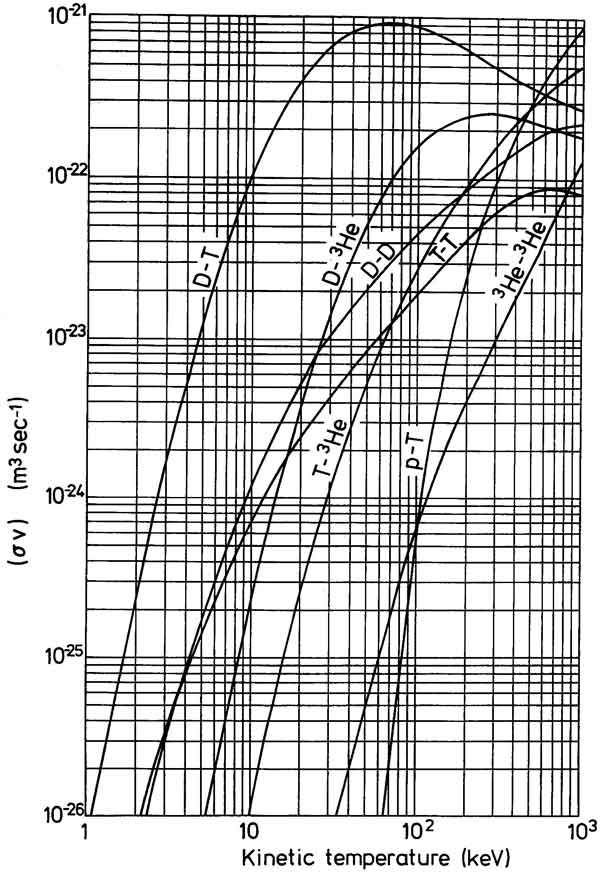 Image 10: Fusion rates for
some fusion reactions
The reaction cross section σ is a measure of the probability of a fusion reaction as the function of the relative velocity of two reactant nuclei. The cross section is expressed in barns, a surface unit with the approximate dimensions of the nucleus of an atom, where 1 barn is 10-24 cm2. When nuclei are reacting with itself (as in our D-D fusion reaction), the product n1n2 becomes ½n2:
At first sight equation V seems quite logical apart maybe from the factor ½, which of course obviously is explained by the fact that when nuclei react with itself the given density of nuclei (i.e. number of particles per unit volume) is reduced to half that nucleus density or with other words, the factor ½ has been introduced into the formula to avoid counting the same interaction twice. The value v may require frame-shifting assuming that one particle is moving and the other is stationary because that is how cross sections were measured in experiments with linear accelerators (reference 23). Fusors are ion accelerators but certainly not linear accelerators with a stationary target and this has nasty consequences for finding a mathematical model as shown in the next paragraph. Equation V should enable to calculate the fusion rate of a Fusor but unfortunately fusion reactions in a Fusor are far from predictable and are difficult to catch in mathematical equations. The reason for this complexity is that particles in a Fusor do not have a fixed kinetic energy and the paths they follow are not straight beams. Particles may be orbiting in circular or elliptical orbits. The kinetic energy of a particle in a Fusor depends on its location in the Fusor, except for those particles orbiting in circular paths, etc. Furthermore, fusion reactions in a Fusor do not occur only in the plasma focus inside the grid but also just outside the grid and possibly also with non-ionized Deuterium gas near the walls of the Fusor. Any attempt to calculate a reaction rate in a Fusor is therefore a simplistic approximation of real values for which different calculation models are available for such an approximation, usually based on different theoretical approaches. One of those methods is shown in the next paragraphs. The velocity v of the colliding nucleus is non-relavistic and can be calculated with the classical formula from equation I, which is mentioned here as:
v = particle velocity in meters per second (m/s) Ek = kinetic energy converted from eV to joules (J) m = mass of the nucleus in kg The cross section for D-D reactions at 10 keV ranges from 2E-4 barn (center collisions) to 1E-3 barn (head-on collisions). A (one) barn is 1E-28 m2 or 1E-24 cm2 as mentioned earlier. Knowing v (converted from m/s to cm/s) and the cross section σ (in cm2) we can calculate the reactivity (σv) expressed in cm3/s. The remaining term of the equation to be calculated is the density of particles (nuclei) per cm3. A simplified method is by assuming that all or at least the majority of the current through the grid is due to ion flow with a charge of +1. We know that one Ampčre equals one Coulomb per second, or 6.24E18 charges per second. We need to compensate for losses caused by the grid by multiplying the charges with the "ion recirculation factor". Assuming that we have a grid transparancy (see below) of 98% than 2% of the ions will be blocked by the grid. This means that an ion will be neutralized by the grid one pass in fifty and therefore the ion recirculation factor would be 50. Another approximation of the recirculation factor can be found by calculating the mean free path of the ions as shown below. The result of multiplying the charges with the ion recirculation factor yields an estimation of the number of ions passing the grid per second. Because we know the diameter of the grid and because we have calculated the velocity of the ions, we can calculate now the the amount of time that an ion is actually in the grid. The overall density in the grid can then be calculated from the time that an ion is in the grid and the amount of ions that pass per second through the grid. The results is expressed as particles per cm3. The calculation rules out time because we multiply duration in seconds (t) ×
number per second (n/t) × volume (cm3) = n/cm3
For a more accurate estimation of the density it is advised to break up the grid sphere volume in two or more concentric spheres (or shells) with in the central region a sphere with the (estimated) dimensions of the Poisor (the visible bright spot), where the ion density is progressively higher. For those who have forgotten their geometry equations to calculate the volume of a sphere:  When the radius of the grid sphere is rg and the radius of the Poisor sphere is rp we find the following equations for calculation of the volumes of the shells:
Next is to calculate for each shell the fusion rate as the product of half the particle density squared and the sigma v values. For the inner shell use the cross section value for the center collisions; for the outer shell(s) use the cross section value for the head-on collisions. Summarize the fusion rates for each shell. Example: Our Fusor operates at 10 kV at a current of 10 mA; it has a grid diameter of 6 cm and the Poisor has an estimated diameter of 4 cm; the cross sections σ for Deuterium at 10 kV are 2E-4 barn for center collisions and 1E-3 barn for head-on collisions. The mass of a deuteron is 3.43583719E-27 kg and the conversion factor from eV to J is 1.60217657E-19. The ion recirculation factor based upon the mean free path is calculated in the next paragraph and found to be 41. This well in line with the rule of thumb calculation based upon the grid transparancy which yields 50 recirculations. An estimated calculation of the recirculation factor was done by applying equation II with a deuteron radius of 2.1413E-15 m, a Fusor pressure of 1E-5 Torr (equals 1.333223684E-3 Pascal), a plasma temperature of 10 keV for which 1eV equals 11604.45 K yielding a plasma temperature of 1.16E8 K, a Boltzmann constant of 1.3806488(13)×10−23 JK-1. With these parameters equation II yields a mean free path length of 8.1719 m, which results in 41 recirculations in a Fusor with a diameter of 20 cm (mean free path length divided by diameter is approximate number of passes or recirculations). In this system the velocity v of the colliding ions is the square root (2 × ((41 × 1.60217657E-19)/3.43583719E-27)) = 61836.633572 m/s or 6183663.3572 cm/s. The factor σv for center collisions is 6183663.3572 cm/s × 2E-4 barn × 1E-24 cm2 = 1.2367E-21 cm3/s and for head on collisions 6183663.3572 cm/s × 1E-3 barn × 1E-24 cm2 = 6.1837E-21 cm3/s. The amount of time that an ion is in the grid is diameter grid divided by the velocity or 6 cm ÷ 6183663.3572 cm/s = 9.7030E-7 s. The number of ions per second equals 10 mA for which 1 A 6.24E18 charges per second times the ion recirculation factor or 1E-3 × 6.24E18 × 41 = 2.558E19 ions/s. The overall density in the grid is amount of time that the ion is in the grid times number of ions per second or 9.7030E-7 s × 2.558E19 ions/s × volume = 2.4820E13 ions in the total volume of the grid. For the poisor shell we find a volume of (r = 2 cm) 4/3 × π × 23 = 33.5 cm3. The ion density in this shell is 2.4820E13 ÷ 33.5 = 7.41E11 ions/cm3. The fusion rate for the poisor shell equals ½ × n2 × (σv) is ½ × (7.41E11)2 n/cm3 × 6.1837E-21 cm3/s = 1698 reactions per second. Similarly, for the grid shell we find a volume of (r = 3 cm) 4/3 × π × (33 - 23) = 79.6 cm3. The ion density in this shell is 2.4820E13 ÷ 79.6 = 3.27E12 ions/cm3. The fusion rate for the grid shell equals ½ × n2 × (σv) is ½ × (3.27E12)2 n/cm3 × 1.2367E-21 cm3/s = 6595 reactions per second. The total fusion rate in the fusor (grid) equals 1698 + 6595 = 8293 reactions per second. More details about this method of calculation can be found in reference 23. For more (different) Fusor math see also reference 24). Abovementioned method(s) for calculating the fusion rate are very rough estimations and a total reaction rate of just over 8000 reactions per second is considered quite sufficient for detection by a neutron detector. A large number of reactions is required here because the number of reactions should exceed the detection limit of the detector sufficiently but it should also be noted that the neutrons from the fusion reactions are randomly emitting from the Fusor in all directions and our detector is just on one fixed spot at a distance from the Fusor. Therefore the majority of these neutrons will not be "seen" by the detector. From the calculations it should be clear that a higher voltage (is more velocity) and a higher current (is more ions) will increase the reaction rate.  Grid Design A grid consists of a sphere wire structure and is connected to the high voltage feedthrough. The diameter size of the grid is usually about 20% of the diameter of the outer wall of the vacuum chamber. Should we have a vacuum chamber with a diameter of 20 cm than the diameter of the grid should be 4 cm. The material for the grid can be stainless steel wire because it permits welding but in order to resist the high temperatures that can occur in the grid also tungsten or tantalum wire is used. Because these materials are more difficult to (spot) weld, a structure based on winding can be used. Sometimes a golf ball is used for winding a grid but when winding is finished it appears to be difficult to remove the golf ball! In reference 25 a link is given to a 3D-printable Fusor grid winding jig, which can be taken apart for easy removal of the grid after winding (image 11).  This particular jig is suitable for winding a grid with a diameter of 1.5" or 38 mm. It requires two 14" or 360 mm lengths of wire (tungsten or tantalum). The crossing intersections can be spot welded for a better rigidity. Experiments in IEC research have demonstrated that fusion efficiency increases when the grid transparancy is greater than 92%. The grid transparancy can be calculated as follows: ((Grid Surface Area - Wire Cross-section Area)/Grid Surface Area)x 100% = %Transparancy for which, assuming that the grid is a perfect sphere: Wire Cross-section Area = Total Length of Wire per Loop x Diameter Wire x Number of Wire Loops = Grid Circumference x Diam. Wire x Number of Wire Loops = 2πrnd and Grid Surface Area = 4πr2 Transparancy = ((4π*r2 -2π*r*n*d)/4π*r2)x100% , which can be reduced to Transparancy = ((r - ½*n*d)/r))x 100% in which: r = radius of the grid n = number of wire loops d = diameter of wire Example: The grid in image 10 has a diameter of 38 mm (a radius of 19 mm), is made of wire with a diameter of 0.23 mm and has 3 loops. The transparancy is according to the formula: (19 -
½*3*0.23)/19 x 100% = 98.2%
The grid tranparancy can be enhanced effectively to exceed the geometrical transparancy by focussing the grid carefully inside the vacuum chamber, i.e. by placing the grid precisely concentric with the outer vacuum chamber sphere. Precise focussing can result in the Fusor operating in "star mode" which causes chanellisation of the ions into distinct rays converging from the center of the grid. The rays (ion paths) go through the grid openings and stay clear from the grid wires. As a result the ion recirculation factor may increase to 100 or higher. The material for the grid wire can be stainless steel but should preferably be tungsten or tantalum. During operation of the Fusor the grid wire becomes hot and stainless steel will not keep its shape but will start sagging. Tungsten is the best choice because of its low vapor pressure, its great tensile strength and its high melting point of 3422°C. However, it is not very suitable for spot welding and therefore an alloy of tungsten and rhenium can be used or tantalum wire. The grid transparancy calculation shows that a thin wire contributes to a high transparancy. It should however be noted that too thin a wire might cause a problem. In a Fusor with a relatively high vacuum and a high voltage potential of 25 kV on the Tungsten wire nothing will happen as long as a plasma short cut (from grid to Fusor wall) does not occur. The resistivity of Tungsten is 5.6*10-8 Ω/m and the resistance of a wire is calculated acoording to: R = (p*l)/w
for whichR = resistance p = resistivity l = length w = width The formula shows that the width (diameter) of the wire is inversely proportional to the resistance, or with other words; a thinner wire has a larger resistance. In case of a plasma short cut our very thin wire might probably light up in a flash to white hot and burn away. Or maybe not?? In a hypothetical example we assume that a plasma short cut occurs at a quarter length of one of the wires (360 mm long) that make our grid, i.e. the path length for the current is 90 mm, the width of the wire is 0.23 mm, the resistivity of the Tungsten wire is 5.6*10-8 Ω/m and the Fusor is operated at 25 kV. We also assume that the plasma has no resistance (which is incorrect but we have no data for a deuterium plasma at given pressures). The formula yields a resistance of the wire path length of 2.2*10-5 Ω, which at 25 kV theoretically might draw a current of about 109 A. This high amount of current has the effect of a true short cut. Fortunately, the Fusor is not capable of supplying such an extreme current as the power supply is limited at 15 mA before it cuts out. In fact, our tungsten wire of 90 mm length and a diameter of 0.23 mm will be emitting maximally a power of 25 kV at 15 mA which equals 375 W. The surface area of the wire is 2πrl or 2*3.14*0.115*90 = 65.031 mm2 or 6.5*10-5 m2 According to the Stefan Boltzmann law for the power per unit area: I = σT4
whereσ = the Boltzmann constant, 5.670373*10-8 W m-2 T-4 , the temperature of the wire will be 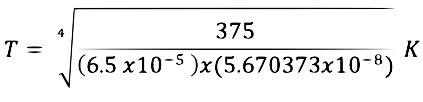 Our example clearly demonstrates that for developing a grid we should take into account the diameter of the wire and the type of material to be chosen. With materials such as tungsten it will be possible to apply a thinner wire and this will improve the grid transparancy,  Radiation Hazards Röntgen (γ) Radiation Operating a Fusor means applying a high voltage to a cathode in a medium or high vacuum environment, which produces thermionically emitted electrons directed outward from the cathode and by colliding with the vacuum enveloppe generate Bremsstrahlung röntgen radiation. Because we use Deuterium as "fuel", which becomes ionized in Deuterons with a single positive charge, the γ-energy of the röntgen radiation in eV is directly related to the potential differential applied. For example a potential difference of 30 kV emits röntgen radiation with an energy up to 30 keV. Generally, it is said that up to a voltage of 25 - 30 kV no röntgen radiation of importance will pass through the (metal) walls of the vacuum chamber. Reference 26 gives information about calculating the amount of röntgen radiation that will penetrate the vacuum chamber wall and we shall use that info for the following calculation. Acoording to reference 27 the mass attenuation coefficient for steel is at 30 keV 8.2 cm2/g and at 10 keV 170 cm2/g. De Beer-Lambert's Law of exponential attenuation is used for calculation of the penetrating flux:
where m = mass attenuation coefficient x = thickness expressed as mass per unit area (g/cm2) The mass density for steel is ρm = 8.0 g/cm3 For a vacuum chamber with a wall thickness of 2 mm: x = ρm × t, where t is the wall thickness, x = 8.0 g/cm3 x
0.2 cm = 1.6 g/cm2
For 30 keV röntgen radiation we find: exp(-8.2×1.6) = 2E-6 or 0.0002% of the radiation will penetrate the vacuum chamber walls, which is indeed of no importance. At 10 kV potential difference or 10 keV röntgen radiation energy we will find even considerably less: 7.4 × E-117%! For calculating what this means as a biological radiation dose we assume that our Fusor runs at 30 keV and 10 mA or an energy of 300 Watt = 300 J/s. Suppose that we have no losses in the system and the röntgen radiation (Bremsstrahlung) is generated by two entities:
In our Fusor each Deuterium has one single charged ion (30 keV) and one electron (30 keV) and therefore the kinetic energy for each is 50% of 300 J/s = 150 J/s. The efficiency for generating röntgen radiation is about 1E-9 and thus we have 150 J/s × E-9 = 1.5E-7 J/s keV X-rays emitting from the plasma focus, of which 0.0002% exits the vacuum chamber = 3E-13 J/s. For an average body mass of 70 kg (see method 1 under Neutron Radiation below) we find an absorbed energy dose of 3E-13 J/s ÷ 70 kg = 4.3E-15 J/kg/s or 1.5E-11 J/kg/h. This equals (conversion: 1 J/kg = 1 Gray) 1.5E-5 µGy/h which converts with a weighting factor of 1 for gamma's to an equivalent tissue dose of 1.5E-5 µSv/h. Compared to the annual limit for professional workers of 20µSv/h (>250 h/y) this is indeed neglectable.  Neutron Radiation It is difficult to measure accurately the total amount of neutrons produced by the fusion reaction as the efficiency for the neutron detector should be known, i.e. taking into account the distance from the detector to the core of the reactor and the factor describing the amount of neutrons hitting the detector in relation to the total amount of neutrons emitted randomly in all directions, etc. Therefore we propose to tackle the problem of calculating the radiation dose from neutrons by two different ways. Method 1 One method is to use the maximum allowable limit for radiation exposure and to calculate the corresponding maximum production rate of reactions in the Fusor. Knowing that maximum production rate enables to calculate more or less up to what high voltage and current the Fusor can safely be operated. This method is explained in reference 28: As a starting point we take the EU dose limit for professional nuclear workers, which is an absorbed dose of 20 µSv/h (< 250 h/year). To compensate for stochastic radiation effects, an energy dependent weighting factor Wr connects the absorbed dose in Gray (Gy to the equivalent tissue dose in Sievert (Sv). The EU commission (reference 29) proposes for neutrons the following equations as a continuous function of the neutron energy: 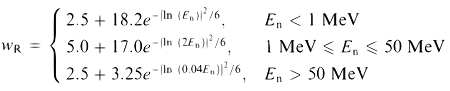 When we substitute the neutron energies of respectively 2.45 MeV and 14.1 MeV in the appropriate equation (for the relevant energy) we find respectively W2.45 = 12.5 and W14.1 = 7.7. The sum of both weighting factors is about 20. Therefore the Fusor is allowed to produce maximally an absorbed dose of 1 µGy/h and this is equivalent with an energy deposition of E-6 J/kg/h. The average body mass of an adult in Europe is just over 70 kg and when we take a body mass of 70 kg as the norm we find that a Fusor energy output of 7E-5 J/h or 1.9E-8 J/s should be considered as acceptable. Neutrons emitted from the Fusor have an energy of respectively 2.45 MeV and 14.1 MeV, which equals respectively 3.93E-13 J and 2.26E-12 J. We divide the maximum allowable fusor output of 1.9E-8 J/s by the neutrons energy and find respectively a maximum allowable fusion rate (# = number of fusions or reactions) of 48500 #/s and 8400 #/s. The outcome may be confusing because we find for one neutron energy a "safe" fusion rate of almost 50,000 fusions per second and for the other neutron energy a "safe" fusion rate of almost 8,500 fusions per second. We should however realise ourselves that both reactions possibly may occur simultaneously. The equations Ia, Ib and II show the D-D reactions that may occur in the Fusor:  The probability that reactions Ia and Ib occur is 50% for each, therefore the emission of neutrons with an energy of 2.45 MeV is realistic. The Tritium formed in reaction Ia will may further react with Deuterons present in the Fusor because the minimum energy required for the D-T reaction is lower than for the D-D reaction and therefore this reaction might also occur. However, the assumption that reactions (Ia,II) and (Ib) occur equally is taken here as a worst case assumption. Worst case because neutrons emitted with an energy of 14.1 MeV are more harmful because of depositing more kinetic energy in tissue. In reality we probably may expect in majority to produce neutrons with an energy of 2.45 MeV because it is expected that most of the formed Tritium decays before being burnt-up by the D-T reaction. With respect to the biological radiation burden the total amount of allowable fusions per time unit is therefore worst case 48,500/s + 8,400/s = approx. 57,000/s. This calculation is valid for an exposure to neutrons directly at the source, i.e. like the Fusor operator was present inside the vacuum chamber during exposure to neutrons produced. Distance reduces the effect of exposure to neutrons but despite such a reduction in neutron flux caused by distance it is not good for your health to be exposed to neutrons. Water contained in the body will moderate (slow down) the neutrons but once an atomic nucleus inside the body is hit, a reaction will occur which produces radioisotopes and reactive free radicals, which stay inside your body until decayed. However, prior to full decay they may be harmful to your health. Method 2 Another method can be used when the neutron flux fom the Fusor is known by converting the neutron flux rate to neutron dose rate for which the calculation is dose rate (rem/h) =
conversion factor ([rem/h]/[neut/cm2s-1]) ×
neutron flux (neutrons per cm2/s)
The conversion factors can be found in a publication by Kwon et al (reference 30). For converting from the rem unit to the currently used unit of Gray: 1 rem/h = 0.01 Gy/h = 10 mGy/h. For our D-D reactions yielding neutrons with energies of 2.45 MeV and 14.1 MeV we find respectively conversion factors of about 1.25E-4 and 2.08E-4. The same arguement about a worst case calculation is equally valid here as in method 1. When measured with the neutron detector and calculated for the distance from the detector to the Fusor operator we find an (assumed) neutron flux of 1000 neutrons/cm2/s at operator level. Because the neutron detector is inside a moderator to slow down fast neutrons to thermic neutrons, which are counted by our detector, our neutron flux consists of (assumed) 50% neutrons with an energy of 2.45 MeV and 50% neutrons with an energy of 14.2 MeV. The dose rate for 2.45 MeV neutrons is calculated as dose rate (mGy/h) = 1.25E-4 (conversion factor) × 500 (50% of neutron flux) × 0.01 (from mrem/h to mGy/h = 0.00104 mGy/h = 1.04 µGy/h. The dose rate for 14.2 MeV neutrons is calculated as dose rate (mGy/h) = 2.08E-4 (conversion factor) × 500 (50% of neutron flux) × 0.01 (from mrem/h to mGy/h = 0.000073 mGy/h = 0.073 µGy/h. The weighting factors for neutrons in order to obtain an equivalent dose in Sv is mentioned before in method 1. By applying the weighting factors W2.45 and W14.1 the total equivalent neutron dose rate is (0.625 × 12.5) + (1.04 × 7.7) = 15.8 µSv/h. This equivalent dose is at a safe level, i.e. below the allowable limit for professional workers of 20µSv/h (>250 h/y).  Some Brainstorming Thoughts We have paid some attention to the theoretical basics of a Farnsworth Fusor, which is a relatively straight forward apparatus. The disadvantage of the design is the fact that it apparently will never reach a break even point due to grid losses. This encourages to start brainstorming and exploring our thoughts in order to develop ideas which possibly can be crafted into original, creative solutions. It is tempting to speculate about fussion ideas with for example p-B11 as fuel, but this is not realistic due to the high peak energy for the reaction. Therefore we shall take the rather simple D-D fusion reaction as a starting point for our considerations. We have seen in the paragraph about D-D fusion that the Lawson Criterion for fusion power is very promising for the D-D reaction. The gross energy gain of the reaction should be reduced with a few eV for tearing D2 gas apart, 13.6 eV for removing an electron from a D2 atom and about 10 to 30 keV for the fusion reaction to find the net gain. The result of this calculus should be multiplied with the efficiency factor, which has some range to vary for still obtaining a nice net energy result. Of course this model is not fully correct because a possibility exists that secundary reactions take place, but still there is sufficient play for exploring the conditions for optimizing our Fusor. Taking a closer look at the Fusor we can observe that basically it is a large gas filled vacuum diode. In order to know more about vacuum diodes and their characteristics we may need to explore publications from the vacuum tube era, which is roughly between 1900 and 1950. The difference between our Fusor as a diode and a conventional gas filled glass diode tube is that in a gas filled diode tube we have a glas envelope containing a cathode consisting usually of a (heated) wire through which a current runs (causing thermionic emissions) and an anode, usually consisting of a flat or circular plate kept at a lower potential than the cathode, whereas in a Fusor we have the grid as the cathode and the (metal) anode is the outer wall (envelope) of the Fusor. Moreover in a Fusor we have a Deuterium gas flow whereas in a vacuum diode the gas is statically present in the envelope. The principle of operating remains the same: in both constructions we find molecules, ions and free electrons present within the envelope. The electron stream from the hot cathode encounters gas molecules on its way to the anode. When an electron hits a gas molecule the energy of the collision might release an electron, leaving the gas particle in an ionized state. The charge of the ion is positive and on its way to the negatively charged cathode it attracts more electrons from the cathode. As we have seen above this is a cummulative (avalanche) process. The velocity of the electrons drifting to the anode and of the ions drifting towards the cathode varies directly with the potential difference between anode and cathode. This is all rather basic stuff and it is evident that this process has limitations in the production of a high density of ions per volume unit. A high density of ions per volume unit is required for improving the efficiency of our Fusor as we have seen in our calculations above but loss of ions caused by collisions with electrons and collisions with the cathode (or: grid) prevent us from increasing the ion density. It seems that we will have to add an addition to our Fusor that leads to a higher ion density. This is, however, not an original idea as other people have already looked for such solutions. An example is Doug Coulter, who states that he produced about 1.5E6 neutrons per second with only 5 Watt input (reference 31). He has sound reasons not to reveal exact details about his setup, but from the information that he gives on his website and on forums it is understood that he makes use of a cylindrical Fusor with a cylindrical grid in combination with a microwave/ECR ion source and a wire to create the ion extraction field. We don't know what other hidden facilities or parameters are being used here, but the concept is promising and in our opinion makes sense. Moreover, it is known that some universities are also experimenting with enhancing IEC devices (Fusors) with ion sources. A microwave/ECR ion source belongs to the family of low-pressure wave-heated plasma generators and generally produces a plasma density of 1010 - 1012 cm-3. Plasma density in general means the density of electrons in the plasma. A slight disadvantage of this system is that it requires relatively high magnetic fields of about 1 kG for which electromagnets are essential. The frequency of 2.45 GHz is e.g. obtained from parts of an old (though working) microwave oven. In our opinion we feel that a better concept can be found in the same family of devices by means of a helicon ion source. The helicon is a device that produces electromagnetic waves propagating in magnetized plasma in the helicon mode. The frequency usually is in the RF range of 1 - 100 MHz and the required magnetic field ranges from 20 - 200 G, which in some designs is obtained with permanent magnets, avoiding electromagnets and expensive power supplies. The typical plasma density obtained in a helicon plasma source is 1011 - 1013 cm-3. The exitation of the helicon wave is provided by an RF antenna which couples to the transverse mode structure across an insulating chamber wall. The electromagnetic wave mode propagates along the plasma column in the magnetic field and is absorbed by plasma electrons. For the schematic overview see image 12: Image 13: Helicon thruster schematic In its simplest form the helicon setup consists of a quartz tube with a ID diameter of about 10 - 30 mm and a length of 200 mm, a number of strong Neodynium magnets (N52), a Deuterium gas inlet, a copper strip or tubing to form the helicon antenna and an RF power source capable of producing up to 100 MHz at 100 Watt. For coupling the RF source to the antenna a matching network will be needed too. The good news is that the total of the RF power source can be obtained around USD 150, consisting of an RF generator (image 14, 15 and 16), a broadband RF amplifier (image 17) and an RF power amplifier (image 18). An ordinary RF signal generator has a relatively low power output and requires for our Fusor ion source purposes a broadband +30 dBm amplification, yielding a signal with about 1.5 Watt output. This is equal to the input requirement for the RF power amplifier, which is used by radio amateurs all over the world for transmitters and therefore they are quite cheap to buy. The bad news is that this set operates only between 80 -170 Mhz, which prevents us from operating larger diameter (>1", >25.4 mm) helicon chambers. Should we require a lower frequency than another RF power amplifier with a range between 2 - 30 MHz and an output of 50W needs to be obtained for about USD 110.  Image 14: 100 MHz signal generator (© seller25812) The signal generator in image 14 has a sinus output of 0 - 100 Mhz in steps of 0.1 Hz, requires 5 VDC input at 1 A and is fully computer controlled by means of Windows software. It can be found on eBay for less than 80 USD, free shipping included.   Image 16 and 17: Examples of RF Generator Software GUI's (© seller25812) In images 16 and 17 we see examples of the pc software control input screens for the RF signal generator of image 14. This software is supplied as downloadable file after purchasing the module.  Image 17: Broadband RF Amplifier (© hamworker) The broadband RF amplifier in image 17 has an operating frequency of 1 - 500 MHz with an input of 0 dBm, 1 mW and an output of 32 dBm, 1.6 W, and requires an operating voltage of 12 V at 0.3A. It can be found on eBay for less than 35 USD, free shipping included.  Image 18: RF Power Amplifier (© flyxy2015) The RF power amplifier in image 18 has a frequency range of 80 -170 MHz, an input of 1 - 1.5 W at 80 - 120 MHz and 3 - 4 W at 120 - 170 MHz and requires 24 - 26 V DC at 5 - 7 A. It can be found on eBay for less than 45 USD, free shipping included. It is a bit of a nuisance that all three components require different supply voltages but this is something that can be accepted considering the relatively low prices and the fact that we do not have to develop and build our own desings. The current drawn by the RF signal generator (5 VDC at 1 A) is too high to be supplied by an ordinary USB port on a pc computer but as the board has a separate power input socket the power can be obtained from a small standard wall plugged power supply. We can further observe that a difference exists in the operating frequency of the microwave/ECR device (2.54 GHz) vs. the helicon device (1 - 100 MHz). Though the results in output of plasma density seem more or less the same, the principle of operation is different. In the microwave/ECR device (ECR stands for Electron Cyclotron Resonance) electrons are powered to move in circles whereas the helicon device operates with ICR (Ion Cyclotron Resonance) propelling ions in circular movements for heating the plasma. As the mass of an electron (9.10938356E-31 kg) is far more lighter than the mass of a Deuteron (3.343583719E-27 kg) we can imagine that a higher resonance frequency is required for propelling electrons than for propelling Deuterons but mostly dimensional charteristics of the plasma chamber (in relation to the resonance characteristic) are also an important factor relating to the operating frequency. The typical frequency that is used for helicon sources is usually 13.56 MHz but smaller sized tubes (e.g. with an inner diameter of <1" / <25.4 mm) will require higher frequencies up to 100 MHz. We are fully aware that our explanations of ECR and ICR are simplified "onto the bare bone" (as is this entire theory page of the website) and therefore we propose that for getting more comprehensive information about these subjects the reader should visit reference 33 for the ICR principles and reference 34 for the ECR principles. As the title of this paragraph tells us ("Some Brainstorming Thoughts") the proposed ion source is far from complete and not that simple as suggested. A number of experiments need to be executed prior to installing a working device. For instance, once the plasma wave exits the helicon source it will diverge and we would like it to stay as condensed as possible before reaching and crossing the grid. Probably the attracting force of the cathode might prevent too much diverging of the ion beam, but we don't know yet. So far, we have not yet developed a solution for that problem but a good guidance in constructing a helicon source can be found in reference 35. and reference 36. Both articles describe the construction of a helicon ion source with relatively simple means. To be continued....... |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Last Updated on: Tue Apr 5 10:27:28 2016 |